在图论中,有一类图是比较特殊图,Regular Graph,我不知道正确翻译是什么,且称为正规图吧,这类图有一个很好的性质,就是图中的每一个Vertex,也就是每一个点所接的边是一样的。
例如,立方体就是有四个点,每个点有三条边(也称之为度)的Regular Graph,简称4k3
In graph theory, a regular graph is a graph where each vertex has the same number of neighbors; i.e. every vertex has the same degree or valency. A regular directed graph must also satisfy the stronger condition that the indegree and outdegree of each vertex are equal to each other.[1] A regular graph with vertices of degree k is called a k‑regular graph or regular graph of degree k. Also, from the handshaking lemma, a regular graph of odd degree will contain an even number of vertices.
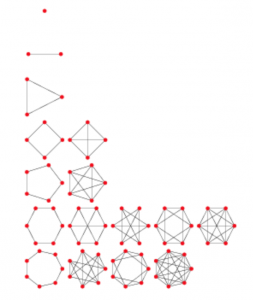
Regular图的示意(来源:http://mathworld.wolfram.com/RegularGraph.html)
现在问题来了,不同点数,不同的度,到底有多少种不同的组合呢,这的确是一个非常有意思的课题
目前可考的,是Jason Kimberley这个人,填了非常多的数字,结果链接如下
http://oeis.org/wiki/User:Jason_Kimberley/A068934
他做出最大结果是
40K36
有8845303172513781271种不同的组合
(修正,实际上不是这个人,而是另一个人在1970年搞出来
@Article{Robinson1983,
author = {R. W. Robinson and N. C. Wormald},
title = {Numbers of cubic graphs},
journal = {Journal of Graph Theory},
year = {1983},
volume = {7},
number = {4},
pages = {463–467},
doi = {10.1002/jgt.3190070412},
file = {:articles/Number of cubic graphs.pdf:PDF},
groups = {Graph Theory},
publisher = {Wiley},
})
太佩服这个人了
基于GENREG这个很古老的程序做的,话说我也联系过这个软件的作者,跟他说我们打算在超算上面跑,他也很认真地回复了哈,给了很好的建议。
不过说实话,这种问题非常难做,需要非常多的机时,而且程序中大量的递归,导致很难并行化,所以还是一步一步来吧。
话说genreg貌似下载链接有问题,我来传一份吧